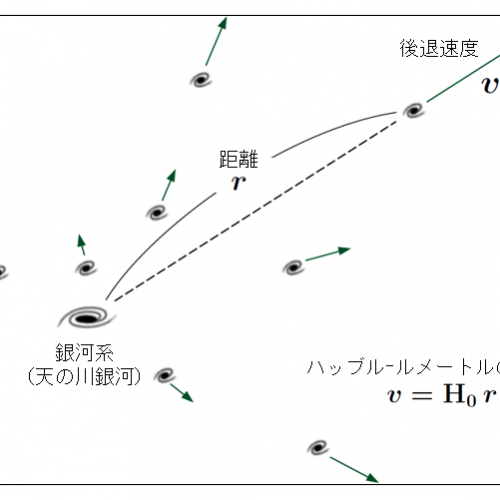
ハッブル–ルメートルの法則

ハッブル–ルメートルの法則（旧称「ハッブルの法則」）とは、現代宇宙論において観測される以下の法則のことを指す。

10メガパーセク以上離れた位置に観測される天体には、地球との相対速度と解釈される赤方偏移が見られる。
このドップラー効果から計算される、様々な銀河の地球からの後退速度は、数百メガパーセク程度の銀河までは地球からの距離にほぼ比例する。

$v$ を天体が我々から遠ざかる速さ（後退速度）、 $D$ を我々からその天体までの距離とすると、

v={H_{0}}\,D

となる。ここで比例定数 $H_{0}$ はハッブル定数 (Hubble constant) と呼ばれ、現在の宇宙の膨張速度を決める。ハッブル定数は時間の逆数の次元 T⁻¹ をもち、通常はキロメートル毎秒毎メガパーセク（記号: km/s/Mpc）が単位として用いられる。この発見は、宇宙は膨張しているものであるとする説を強力に支持するものとなった。

1929年にエドウィン・ハッブルが論文で発表したため、この法則は「ハッブルの法則」の名称で広く世に知られたが、1922年に現在「フリードマン方程式」として知られている一連の方程式を発表したアレクサンドル・フリードマンによって一般相対性理論の式から導き出されたのが最初である。1927年にはジョルジュ・ルメートルも宇宙の膨張を提案し、膨張率の推定値を提示していたが、フランス語のマイナーな雑誌に掲載されたため、その時点ではまだ注目されていなかった。なお、ルメートルはスライファーとハッブルの観測データを用いている。2018年8月に開催された第30回国際天文学連合総会で、ルメートルの功績を顕彰するため、ハッブルの法則を「ハッブル＝ルメートルの法則」 (Hubble-Lemaître law) と呼ぶことを推奨する決議案が提出された。2018年10月26日に締め切られた投票の結果、この決議案は約78%の賛成多数を以て採択された。

ハッブルパラメータの変化

ハッブル定数は、定数と呼ばれているが、時間と共に変化しうる。時間の関数としてのハッブル定数はハッブルパラメータ (Hubble parameter) と呼び、 $H$ や $H(t)$ で表す。観測で求められるハッブル定数

H_{0}=H(0)

は、正確には「現在のハッブルパラメータ」である。

エドワード・アーサー・ミルンが導出した、宇宙膨張が加速も減速もしないミルン宇宙では、ハッブルパラメータはビッグバンからの経過時間に反比例して減少する。速度 $v$ が一定のまま距離 $D$ だけが増加するからである。

一方、定常宇宙論ではハッブルパラメータは一定である。宇宙膨張は指数関数的に加速し（過去にさかのぼると減速し）、過去にいくらさかのぼってもビッグバンは起こらない。

「距離」「速度」の定義

近くの銀河だけを見ているときは「距離」と「速度」の定義は自明だが、遠くの銀河についてはそれらの定義が問題となる。

ハッブル–ルメートルの法則が成り立つ「距離」とは、共動距離、つまり、その銀河の現在位置までの距離である。「速度」とは、その時間微分である。観測上、遠方の天体ほど、ハッブル–ルメートルの法則に従わなくなる。これは光速が有限なため観測上遠方の天体が過去の距離（宇宙論的固有距離）と速度を表し、かつ過去のハッブル定数が現在のハッブル定数と異なるからである。

銀河までの共動距離を $D(t)$ で表すと、ハッブル–ルメートルの法則は次のように表せる。

{\frac {d}{dt}}D=H\!(t)\,D(t)

距離として光路距離、つまり、光が届く所要時間に光速度を掛けた値を使うと、

{\frac {d}{dt}}D_{\mathrm {L} }=c\,{\frac {z}{1 z}}

（ $z$ は赤方偏移）が成立するが、ミルンの宇宙以外では遠くの銀河の光路距離に対してハッブル–ルメートルの法則は成り立たない。

ハッブル定数の値

銀河の後退速度は銀河からの光のスペクトルの赤方偏移を調べることによって容易に決定できるが、距離の決定は、現在のところ、様々な算出方法を総合して割り出すしかないため、正確な値を求めることは困難である。そのためハッブル定数は不確かなものとなっている。

つい最近まで、ハッブル定数の見積もりには 50–100 km/s/Mpc という非常に大きな不確かさがあった。

2008年に公表された WMAP による初期の観測では、70.5±1.3 km/s/Mpc という値が与えられていた。その後、NASAの赤外線宇宙望遠鏡スピッツァーによる遠赤外線の観測から 74.3±2.1 km/s/Mpc という値が得られたが、2012年に、NASAの人工衛星WMAPなどの観測による 69.32±0.80 km/s/Mpc という値が与えられた。

2013年には、プランクの観測結果により 67.15±1.2 km/s/Mpc という新しい値が与えられた。

2017年現在、70.0 12.0
−8.0 km/s/Mpc という値が公表されている（下記の表参照）。

ハッブル時間とハッブル距離

ハッブル定数の逆数は $T$ （時間）の次元を持ち、ハッブル時間と呼ばれる。

t_{\mathrm {H} }={\frac {D}{v}}={\frac {1}{H_{0}}}

先のハッブル定数の値を使うと、ハッブル時間は138億年である。宇宙の年齢 $t_{0}$ は、ミルン宇宙ではハッブル時間に等しいが、実際は加速や減速があるので、ハッブル時間とは異なる。観測で得られた宇宙論パラメータを使うと、実際の宇宙は加速と減速を繰り返した結果、宇宙の年齢はハッブル時間とほとんど同じ137億年となる。ただし、ハッブル時間そのものに物理的意味はない。

光速度をハッブル定数で割った値、つまり、光速度とハッブル時間の積を、ハッブル距離