トンネル効果

トンネル効果（トンネルこうか、英: tunnelling effect）は、量子力学において、波動関数がポテンシャル障壁を超えて伝播する現象である。

20世紀初頭に予言され、20世紀半ばには広く認知される物理現象となった。トンネル効果は、ハイゼンベルクの不確定性原理と、物質における粒子と波動の二重性を用いて説明できる。

トンネル効果は、原子核崩壊や核融合など、いくつかの物理現象において欠かせない役割を果たしている。また、トンネルダイオード、量子コンピュータ、走査型トンネル顕微鏡、フラッシュメモリなどの装置において応用されているという意味でも重要である。

歴史

1901年、ロバート・フランシス・イアハートは、電極間の距離を測定することができるマイケルソン干渉計を用いて、非常に近接した電極間における気体の電気伝導性を研究していたところ、予想に反して大きな電流が流れることを発見した。1911年から1914年にかけて、当時大学院生であったフランツ・ロターは、イアハートの手法を応用して、電極間の距離を制御及び測定する方法について研究した。ロターは、感度の高い検流計を用いて、電極間を流れる電流を測定することにより、電極間の距離を測定する方法を発案した。1926年、ロターは 26 pA（ピコアンペア） の感度をもつ検流計を用いて、高真空の環境下において、近接させた電極間を流れる電流を計測した。

トンネル効果に係る理論は、放射能及び原子核物理学の研究によって発展した。フリードリッヒ・フントは1927年、二重井戸ポテンシャルの基底状態の研究において、トンネル効果について初めて言及している。1928年、ジョージ・ガモフと、彼とは独立にロナルド・ガーニーとエドワード・コンドンにより、アルファ崩壊の説明において、トンネル効果が応用された。彼らは、核ポテンシャルをモデル化したシュレーディンガー方程式を解き、粒子の半減期と、放出されるエネルギーとの関係式が、トンネル効果の起こる確率と直接関係していることを導いた。

マックス・ボルンは、ガモフのセミナーに参加した際に、トンネル効果が原子核物理学の範囲内に留まらず、もっと普遍的な現象であることに気付いた。その直後、両グループは、トンネル効果によって粒子が原子核に取り込まれることについて考察した。1957年までに、半導体の研究とトランジスタやダイオードの開発を通じて、電子のトンネル効果が広く認知されるようになった。江崎玲於奈、アイヴァー・ジェーバー、ブライアン・ジョゼフソンは超伝導性クーパー対のトンネル効果を予言し、1973年のノーベル物理学賞を受賞した。2016年、水の量子トンネリングが発見された。

基礎

トンネル効果は、非常に微細な領域で発生する現象であるため、我々が直接知覚することはできない。また、古典力学では説明することができず、量子力学により取り扱う必要がある。

例えば、ポテンシャル障壁に向かっている粒子を、丘を転がり上がるボールに喩えて考えた時、古典力学においては、障壁を乗り越えるだけのエネルギーを粒子が持っていない限り、粒子は障壁の向う側には到達できない。つまり、丘を乗り越えるだけのエネルギーを持たないボールは、途中で止まり丘を転がり落ち戻っていく。別の喩えを用いれば、壁を貫通するだけのエネルギーを持たない銃弾は跳ね返されるか、壁の中で止まる。ところが、量子力学においては、ある確率で粒子は障壁を貫通する。この場合、「ボール」は環境からエネルギーを「借りて」丘を乗り越え、反射電子のエネルギーを高くすることによってそれを返済する。

このような違いは、量子力学における粒子と波動の二重性に起因する。この二重性により導かれるハイゼンベルクの不確定性原理によれば、粒子の位置と運動量は確定することができない。このことは、粒子はぼんやりとした雲のように存在している（存在確率に空間的な広がりがある）ことを意味しており、また、その確率が厳密に0（もしくは1）になるような解はない。したがって、障壁に粒子が衝突する時、障壁を挟んだ反対側には粒子の存在確率があり、障壁が薄ければ薄いほど、その存在確率は無視できないものとなる。

トンネリング問題

波動関数は系のすべての情報を持っている。系の波動関数を得るには、シュレーディンガー方程式（あるいはそれと等価な方程式）を解析的ないし数値的に解く必要がある。 通常、波動関数は位置の関数として表されるが、この場合、波動関数はある場所に粒子を見出す確率を与える（2乗絶対値が確率密度関数に対応する）。障壁を高くもしくは広くする極限をとれば、透過する確率は下がる。

矩形ポテンシャル障壁のような単純な模型においては解析解が存在するが、一般には解析解を得ることは難しい。 そのため、系に応じたいくつかの仮定の下で近似を行い、近似的な解析解または数値解を得る手法が研究されている。

例えばプランク定数が系の作用に比べて充分小さいと見なせる場合、シュレーディンガー方程式はハミルトン–ヤコビ方程式に帰着する。 WKB近似は、系がこのような準古典的振る舞いをすると仮定して近似解を求める手法である。

関連する現象

量子トンネルと同じ振舞いをしめし、量子トンネルにより正確に説明できる現象がいくつか存在する。例として、古典的な波動・粒子関連性やエバネッセント波カップリング（光へのマクスウェル方程式の適用）、音響学における弦に発生する波への非拡散波動方程式の適用などがある。エバネッセント波カップリングは近年にいたるまで、量子力学では単に「トンネリング」と呼ばれていたが、別の文脈でこう呼ばれるようになった。

これらの効果は矩形ポテンシャル障壁の場合と同じようにモデル化することができる。このような場合、波の伝播が一様もしくはほぼ一様な媒質と、それとは伝播が異なるもうひとつの媒質が登場し、媒質B領域が一つ、媒質A領域が二つあるような形で説明できる。シュレーディンガー方程式を用いた矩形ポテンシャル障壁の解析は、媒質Aでは進行波解が得られ、媒質Bでは実指数関数解が得られるような別の効果に対しても有効である。

光学では、媒質Aは真空で媒質Bはガラスである。音響学では、たとえば媒質Aは流体、媒質Bは固体とおける。この両方で、媒質A領域では粒子の総エネルギーがポテンシャルエネルギーよりも大きく、媒質Bがポテンシャル障壁となっている。この場合、入射波と反射波、透過波が得られる。さらに多くの媒質および障壁を設けることもあり、障壁が非連続ではない場合もある。このような場合は近似が便利である。

スピン偏極共鳴トンネル効果

スピン偏極共鳴トンネル効果はトンネル効果の一種である。2002年に産業技術総合研究所エレクトロニクス研究部門と科学技術振興事業団の研究チームによる単結晶ナノ構造電極を持つ新型TMR素子の開発過程において、室温でTMR素子の電極内部に量子井戸準位を生成すると磁気抵抗が巨大な振動を起こす現象、すなわちスピン偏極共鳴トンネル効果が発見された。室温で作動するスピントランジスタの実現が期待される。

応用

量子トンネリングは障壁の厚さがおよそ 1–3 nm 以下の場合に起こるが、これはいくつかの重要な巨視的な物理現象の原因となっている。たとえば、VLSIにおいて電力損失および発熱の原因となり、ひいてはコンピュータチップのサイズダウン限界を定めている漏れ電流の原因は量子トンネリングである。

恒星内での核融合

恒星内での核融合にとっても量子トンネルは重要である。恒星の核における温度と圧力をもってしても、クーロン障壁を乗り越えて熱核融合を引き起こすためには十分でない。しかし、量子トンネルのおかげでクーロン障壁を通り抜ける確率が存在する。この確率は非常に低いが、恒星に存在する原子核の数は莫大であり、数十億年にもわたって定常的に核融合が続くこととなる。ひいては、生物が限られたハビタブルゾーンの中で進化できるための前提条件となっている。

放射性崩壊

放射性崩壊とは不安定原子核が粒子とエネルギーを放出して安定な原子核へと変化する過程である。この過程は粒子が原子核内から外へトンネリングすることにより生じている（電子捕獲の場合は電子は外から内へトンネリングしている）。量子トンネルが初めて適用された例であり、初めての近似でもある。放射性崩壊は宇宙生物学上も重要である。ハビタブルゾーン外で日光の十分に届かない領域（たとえば深海底）で生物が長期間に渡って生存できる環境が放射性崩壊、ひいては量子トンネリングによって実現される可能性が指摘されている。

星間雲における宇宙化学

量子トンネル効果を考慮することにより、分子状水素や水（氷）、および生命の起源として重要なホルムアルデヒドなどの様々な分子が星間雲において宇宙化学的に合成されている理由を説明できる。

量子生物学

量子生物学において、無視できない量子効果の筆頭として量子トンネル効果が挙げられる。ここでは、電子トンネリングとプロトントンネリングの二つが重要となる。電子トンネリングは多くの生化学的酸化還元反応（光合成、細胞呼吸）および酵素反応のキーファクターであり、またプロトントンネリングはDNA自発変異におけるキーファクターである。

DNA自発変異は通常のDNA複製時において、特に重要なプロトンが確率の低い量子トンネリングを起こすことによって生じ、これを量子生物学では「プロトントンネリング」と呼ぶ。通常のDNA塩基対は水素結合で会合している。水素結合に沿って見ると、二重井戸ポテンシャル構造が生じており、片方がより深くもう片方が浅い非対称となっていると考えられている。このため、プロトンは通常深い方の井戸に収まっていると考えられる。変異が起こるためにはプロトンは浅い方の井戸にトンネル抜けする必要がある。このようなプロトンの通常位置からの移動は互変異性遷移と呼ばれる。このような状態でDNAの複製が始まった場合、DNA塩基対の会合則が乱され、変異が起こりうる。ペル＝オロフ・レフディンが初めて二重螺旋中における自発変異を取り扱うこの理論を構築した。その他の量子トンネル由来の変異が老化や癌化の原因であると考えられている。

電界放出

電子の電界放出は半導体物理学や超伝導体物理学に関連する。これは電子がランダムに金属表面から飛び出すという点で熱電子放出と似ている。熱電子放出では互いに衝突しあう粒子がエネルギー障壁を越えるエネルギーを獲得して放出されるが、電界放出では強い電界をかけることによってエネルギー障壁が薄くなり、電子が原子状態からトンネル抜けすることによって電子の放出が起こる。したがって、電流は電界におおよそ指数関数的に依存する。フラッシュメモリーや真空管、電子顕微鏡などにおいて重要である。

トンネル接合

非常に薄い不導体を二つの導体で挟み込むことによって単純な障壁を作ることができる。これをトンネル接合とよび、量子トンネルの研究に用いられる。ジョセフソン接合は超伝導と量子トンネルを利用するジョセフソン効果を起こすための構造である。これは電圧と磁場の精密計測、および多接合太陽電池に応用できる。

トンネルダイオード

ダイオードとは、電流を一方向にしか流さない半導体素子である。この素子はn型とp型の半導体の接合面に生じる空乏層に依存して動作している。半導体のドープ率を極めて高くすると、空乏層が量子トンネリングが生じるほど薄くなる。すると、順バイアスが小さい場合にはトンネリングによる電流が支配的となる。この電流はバイアス電圧がp型およびn型の伝導帯エネルギー準位が一致するような値のとき最大となる。バイアス電圧をさらに増していくと、伝導体がもはや一致しなくなり通常のダイオードと同様の動作を示すようになる。

トンネル電流は急速に低下するため、電圧が増すと電流が減るような電圧領域を持つトンネルダイオードを作成することが可能である。このような特異的特性は、電圧の変化の速さに量子トンネル確率の変化が追従できるような高速素子などにおいて応用されている。

共鳴トンネルダイオードは同じような結果を達成するが、量子トンネリングを全く異る方法で応用している。このダイオードは伝導体のエネルギー準位が高い薄膜を複数近接して配置することにより、特定の電圧で大きな電流が流れる共鳴電圧を持つ。このような配置により最低エネルギー準位が不連続に変化する量子ポテンシャル井戸が形成される。このエネルギー準位が電子のエネルギー準位よりも高い場合はトンネリングは起こらず、逆バイアスのかかったダイオードのように動作する。二つのエネルギー準位が一致したとき、電子は導線で繋がれたかのように流れる。電圧をさらに高くするとトンネリングが起こらなくなり、あるエネルギー準位からはまた通常のダイオードのように動作しはじめる。

トンネル電界効果トランジスタ

ヨーロッパの研究プロジェクトにより、ゲート（チャネル）を熱注入ではなく量子トンネリングで制御することにより、ゲート電圧を ~1 ボルトから 0.2 ボルトに低減し、電力消費量を 100分の1以下に抑えた電界効果トランジスタが実証された。このトランジスタをVLSIチップにまでスケールアップすることができれば、集積回路の電力性能効率を大きく向上させることができる。

量子伝導

電気伝導におけるドルーデモデルは金属中の電子の伝導について優れた予言を行うが、電子の衝突時の性質について量子トンネルを考慮して改良することができる。自由電子波束が等間隔に並んだ長い障壁の列に遭遇すると、反射された波束と透過する波束が均一に干渉して透過率が100%となる場合がある。この理論によれば、正に帯電した原子核が完全な長方形格子を構成する場合、電子は金属中を自由電子のようにトンネリングし、極めて高い伝導度を示すこと、および金属中の不純物によりこれが大きく阻害されることが予言される。

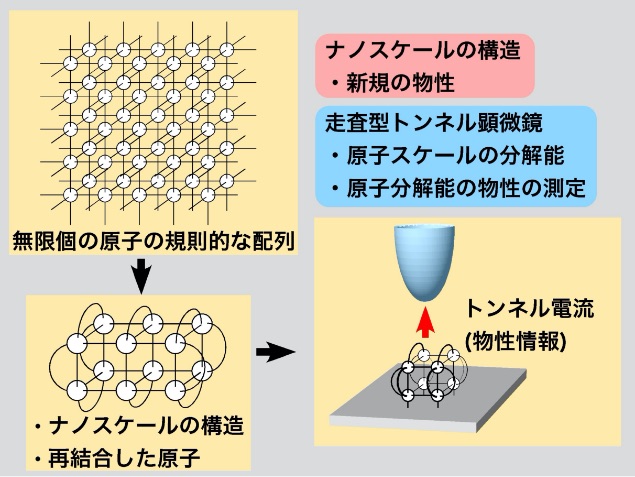
走査型トンネル顕微鏡

ゲルト・ビーニッヒとハインリッヒ・ローラーにより発明された走査型トンネル顕微鏡 (STM) は、金属表面の個々の原子を判別できる画像を撮像できる。これは量子トンネル確率が位置に依存する性質を利用したものである。バイアス電圧を掛けたSTM針の針先が伝導体表面に近付くと、針から表面へと電子がトンネリングし、これを電流として計測することができる。この電流により、針と表面の距離を計測できる。圧電素子に印加する電圧を制御して、針が表面と一定距離を保つように伸び縮みさせることができる。圧電素子に印加した電圧の時間変化を記録すれば、表面の像を得ることができる。STMの精度は 0.001 nm、すなわち原子直径の 1% に及ぶ。

超光速

スピンゼロ粒子がトンネリングするとき、光速を超えて移動することがある。これは一見相対論的因果律に反しているように見えるが、波束の伝播を詳しく解析すると、相対性理論に反していないことがわかる。1998年、フランシス・E・ローはゼロ時間トンネリングについてのレビューを執筆した。フォノン、光子、電子のトンネル時間についてのより新しい実験データはギュンター・ニムツにより発表されている。

量子トンネルの数学的表現

以下の節では量子トンネルの数学的公式化について論じる。

シュレーディンガー方程式

一粒子・一次元の時間非依存シュレーディンガー方程式は以下のように書ける。

${\displaystyle -{\frac {\hbar ^{2}}{2m}}{\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\Psi (x) V(x)\Psi (x)=E\Psi (x)}$

${\displaystyle {\frac {d^{2}}{dx^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)\Psi (x)\equiv {\frac {2m}{\hbar ^{2}}}M(x)\Psi (x),}$

ここで ${\displaystyle \hbar }$ はディラック定数、m は粒子質量、x は粒子の動く方向に沿って測った位置、Ψ はシュレーディンガーの波動関数、V は粒子はポテンシャルエネルギー、E は x 方向に運動する粒子のエネルギー、M(x) は広く受け入れられている物理学的な名前はないが V(x) − E により定義される量である。

このシュレーディンガー方程式の解は M(x) が正か負かによって異る形式をとる。M(x) が定数で負のとき、シュレーディンガー方程式は次のように書ける。

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)=-k^{2}\Psi (x),\;\;\;\;\;\;\mathrm {where} \;\;\;k^{2}=-{\frac {2m}{\hbar ^{2}}}M.}$

この方程式の解は位相定数が k または -k の進行波を表わす。一方、M(x) が定数で正のとき、シュレーディンガー方程式は次のように書ける。

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\Psi (x)={\frac {2m}{\hbar ^{2}}}M(x)\Psi (x)={\kappa }^{2}\Psi (x),\;\;\;\;\;\;\mathrm {where} \;\;\;{\kappa }^{2}={\frac {2m}{\hbar ^{2}}}M.}$

この方程式の解はエバネッセント波を表わす。M(x) が位置によって変化する場合も、M(x) が負か正かによって同じ挙動の違いが生じる。したがって、M(x) の符号が媒質の性質を表わしている。M(x) が負ならば上で説明した媒質Aに相当し、正ならば媒質Bに相当する。したがって、M(x) が正の領域が M(x) が負の領域に挟まれている場合に障壁が形成され、エバネッセント波結合が生じうる。

M(x) が x によって変化する場合は数学的取扱が困難であるが、通常は実際の物理系に対応しない例外的な特殊例もいくつかある。教科書に載っているような半古典近似法に関連した議論は次節で述べる。完全で複雑な数学的取扱に関しては、Fröman & Fröman 1965を参照されたい。彼らの手法は教科書には載っていないが、定量的には小さな影響しかない補正である。

WKB近似

波動関数を以下のようにある関数の指数関数を取って表わすものとする。

${\displaystyle \Psi (x)=e^{\Phi (x)}}$${\displaystyle \Phi ''(x) \Phi '(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right).}$

${\displaystyle \Phi '(x)}$ は実部と虚部に分けることができる。

${\displaystyle \Phi '(x)=A(x) iB(x)}$ ここで、A(x) および B(x) は実値関数とする。

上の第二式にこれを代入し、左辺の虚部が零となる必要があることを用いると、次を得る。

${\displaystyle A'(x) A(x)^{2}-B(x)^{2}={\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$.

この方程式を半古典近似を用いて解くには、各関数を ${\displaystyle \hbar }$ の羃級数に展開する。この方程式の実部を満たすためには、羃級数が少なくとも ${\displaystyle \hbar ^{-1}}$ から始まる必要があることがわかる。古典極限の振舞いを良くするためにはプランク定数の次数はなるべく高い方がよいので、次のように置くこととする。

${\displaystyle A(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}A_{k}(x)}$

${\displaystyle B(x)={\frac {1}{\hbar }}\sum _{k=0}^{\infty }\hbar ^{k}B_{k}(x)}$

また、最低次の項については次のような拘束が課せられる。

${\displaystyle A_{0}(x)^{2}-B_{0}(x)^{2}=2m\left(V(x)-E\right)}$

${\displaystyle A_{0}(x)B_{0}(x)=0}$

ここで、二つの極端な場合について考察する。

Case 1

振幅の変化が位相に比べて遅い場合、${\displaystyle A_{0}(x)=0}$ および

${\displaystyle B_{0}(x)=\pm {\sqrt {2m\left(E-V(x)\right)}}}$

は古典的運動に相当する。次の次数までの項を解くと、次を得る。

${\displaystyle \Psi (x)\approx C{\frac {e^{i\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}} \theta }}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(E-V(x)\right)}}}}$

Case 2

位相の変化が振幅に比べて遅い場合、${\displaystyle B_{0}(x)=0}$ および

${\displaystyle A_{0}(x)=\pm {\sqrt {2m\left(V(x)-E\right)}}}$

はトンネリングに相当する。次の次数までの項を解くと、次を得る。

${\displaystyle \Psi (x)\approx {\frac {C_{ }e^{ \int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}} C_{-}e^{-\int dx{\sqrt {{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}{\sqrt[{4}]{{\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}}}}$

どちらの場合でも、近似解の分子を見れば古典的折り返し点 ${\displaystyle E=V(x)}$ 付近で破綻することが瞭然だろう。このポテンシャルの丘から遠いところでは、粒子は自由に振動する波と類似の振る舞いを示す。ポテンシャルの丘のふもとでは、粒子の振幅は指数関数的に変化する。これらの極限における振る舞いと折り返し点を考慮すると、大域解を得ることができる。

はじめに、古典的折り返し点を x₁ とし、${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)}$ を x₁ 周りの羃級数で展開する。

${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1}) v_{2}(x-x_{1})^{2} \cdots }$

この初項のみを採れば線形性が保証される。

${\displaystyle {\frac {2m}{\hbar ^{2}}}\left(V(x)-E\right)=v_{1}(x-x_{1})}$

この近似を用いると、x₁ 近傍について次の微分方程式を得る。

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\Psi (x)=v_{1}(x-x_{1})\Psi (x)}$

これはエアリー関数を用いて解くことができる。

${\displaystyle \Psi (x)=C_{A}Ai\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right) C_{B}Bi\left({\sqrt[{3}]{v_{1}}}(x-x_{1})\right)}$

この解を全ての古典的折り返し点について用いることで、上の極端な場合の解を繋ぐ大域解を得ることができる。古典的折り返し点の片側で2つの係数が与えられれば、逆側の2つの係数はこの局所解を用いてそれらを繋ぐことで決定することができる。

したがって、エアリー関数解は適切な極限の元で sin, cos 関数と指数関数に漸近する。${\displaystyle C,\theta }$, ${\displaystyle C_{ },C_{-}}$ の関係式は次のように得られる。

${\displaystyle C_{ }={\frac {1}{2}}C\cos {\left(\theta -{\frac {\pi }{4}}\right)}}$

${\displaystyle C_{-}=-C\sin {\left(\theta -{\frac {\pi }{4}}\right)}}$

これらの係数が決まれば、大域解が得られる。したがって、一つのポテンシャル障壁をトンネリングする粒子の透過係数は以下のように得られる。

${\displaystyle T(E)=e^{-2\int _{x_{1}}^{x_{2}}\mathrm {d} x{\sqrt {{\frac {2m}{\hbar ^{2}}}\left[V(x)-E\right]}}}}$

ここで、x₁, x₂ はポテンシャル障壁にある二つの古典的折り返し点である。

矩形障壁の場合は、この式は次のように簡単化できる。

${\displaystyle T(E)=e^{-2{\sqrt {{\frac {2m}{\hbar ^{2}}}(V_{0}-E)}}(x_{2}-x_{1})}={\tilde {V}}_{0}^{-(x_{2}-x_{1})}}$

出典

関連文献

• Fröman, N.; Fröman, P.-O. (1965). JWKB Approximation: Contributions to the Theory. Amsterdam: North-Holland 
• Razavy, Mohsen (2003). Quantum Theory of Tunneling. World Scientific. ISBN 981-238-019-1 
• Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X 
• James Binney and Skinner, D. (2010). The Physics of Quantum Mechanics: An Introduction (3rd ed.). Cappella Archive. ISBN 1-902918-51-7 
• Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5 
• Vilenkin, Alexander (2003). “Particle creation in a tunneling universe”. Physical Review D 68 (2): 023520. arXiv:gr-qc/0210034. Bibcode: 2003PhRvD..68b3520H. doi:10.1103/PhysRevD.68.023520. 
• H.J.W. Müller-Kirsten (2012). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral, 2nd ed.. Singapore: World Scientific 

関連項目

外部リンク

• Animation, applications and research linked to tunnel effect and other quantum phenomena (Université Paris Sud)
• Animated illustration of quantum tunnelling
• Animated illustration of quantum tunnelling in a RTD device
• 『トンネル効果』 - コトバンク